Energy in SHM

A particle of mass $m$ oscillates in Simple Harmonic Motion between points $x_1$ and $x_2$, the equilibrium position being $O$. Which of the following graphs represents the variation of its potential energy $\left(U\right)$ with respect to its position?

A particle executing SHM with an amplitude $\mathrm{A}$. The displacement of the particle when its potential energy is half of its total energy is

If $x$ is the displacement of the particle from the mean position, the total energy of a particle executing simple harmonic motion is

The total energy of the particle executing Simple Harmonic Motion is 

Graph of kinetic energy in terms of displacement in $SHM$ :-

(i) At what displacement of particle executing $SHM,$ has maximum kinetic energy.

Which of the given is graph of the square of cosine function?

A particle is executing simple harmonic motion with a time period T. At time t = 0, it is at its position of equilibrium. The kinetic energy - time graph of the particle will look like:

The kinetic energy of a particle executing S.H.M. is $16 \mathrm{J}$ when it is at its mean position. If the amplitude of oscillations is $25 \mathrm{cm}$, and the mass of the particle is $5.12 \mathrm{kg}$, then the time period of the oscillation is

Which of the following is correct about Simple Harmonic Motion (SHM) along a straight line?

For a simple pendulum, a graph is plotted between its kinetic energy ($KE$) and potential energy ($PE$) against its displacement $d$. Which one of the following represents these correctly?
(graphs are schematic and not drawn to scale)

A point particle is acted upon by a restoring force $-k{x}^3.$ The time period of oscillation is $T$ when the amplitude is $A.$ The time period for an amplitude $2A$ will be:

The ratio of kinetic energy at a mean position to potential energy at $\frac{A}{2}$ of a particle performing $\mathrm{SHM}$ is

$U$ is the potential energy of an oscillating(SHM) particle and $F$ is the force acting on it at a given instant. Which of the following is correct?

(Given $x$ is displacement of the particle)

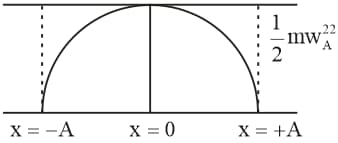
A particle of mass $m$ oscillates with simple harmonic motion between points $x_1$ and $x_2$, the equilibrium position being at $O$. Its potential energy is plotted. It will be as given below in the graph,

A block of mass $1 \mathrm{kg}$ tied to a long spring of spring constant $100 \mathrm{N} {\mathrm{m}}^{-1}$ is at rest on a horizontal frictionless surface. The block is pulled through a distance $5 \mathrm{cm}$ from its equilibrium position and released. Then the total energy of the block when it is at a distance $4 \mathrm{cm}$ from the equilibrium position is

The potential energy of a simple harmonic oscillator of mass $2 \mathrm{kg}$ at its mean position is $5 \mathrm{J}$. If its total energy is $9 \mathrm{J}$ and amplitude is $1 \mathrm{cm}$, then its time period is

The $KE$ and $PE$ of a particle executing simple harmonic motion with amplitude $A$ has ratio $2:1$, then its displacement is,

At what time $PE$ will be equal to half of the total energy $\left(TE\right)$ in SHM of time period $T$.

A simple pendulum of length $L$ has mass $M$ and it oscillates freely with amplitude $A$. At extreme position, its potential energy is ($g$= acceleration due to gravity)

Obtain an expression for potential energy of a particle performing$\mathrm{S}.\mathrm{H}.\mathrm{M}.$ What is the value of potential energy at
(i) mean position
(ii) extreme position?